Pengertian
Distribusi Peluang
Distribusi peluang adalah
sebaran kemungkinan terjadinya variable acak tertentu. Variable acak adalah
peristiwa yang diharapkan akan terjadi, yang biasanya dilambangkan dengan X.
Atau, suatu bilangan yang ditentukan oleh peristiwa yang dihasilkan dari eksperimen.
Distribusi Peluang Untuk Variabel Diskrit
a) Distribusi
Binomial
Yaitu distribusi peluang untuk variable random
diskrit. Mempunyai ciri-ciri sebagai berikut:
1. Setiap percobaan bersifat independent atau
dengan pengembalian.
2. Setiap percobaan tunggal menghasilkan dua
kejadian (dikotomos) yaitu, gagal dan sukses. Sehingga, peluangnya hanya ada dua yaitu :
1. Peluang Sukses (p)
2. Peluang Gagal (q)
Dimana jumlah p+q=
1.
Jumlah
sampelnya hanya sedikit, dimana sampelnya tidak lebih dari 30, yaitu 1 sampai
dengan 30.
Rumus :

Keterangan :
X = Variable acak (peristiwa) yang diharapkan akan
terjadi.
x = Banyaknya peristiwa yang diharapkan.
n = Banyaknya percobaan.
p = Peluang sukses yang dihitung dari satu kali
percobaan.
q = Peluang gagal, dimana q=1-p.
b) Distribusi Posisson
Yaitu distribusi peluang
untuk variable random diskrit. Mempunyai ciri-ciri sebagai berikut:
1. Setiap
percobaan bersifat independent atau dengan pengembalian.
2. Setiap percobaan tunggal menghasilkan dua kejadian (dikotomos)yaitu,
gagal dan sukses. Sehingga, peluangnya hanya ada dua yaitu :
·
Peluang Sukses
(p)
·
Peluang Gagal
(q) Dimana jumlah p+q= 1.
Peluang sukses biasanya
sangat sedikit.
Ukuran sampel atau populasinya
sangat besar. Yaitu n > 30
Biasa disebut juga distribusi
industri.
c) Distribusi Hipergeometris
Distribusi hipergeometrik juga
termasuk distribusi teoretis yang menggunakan variabel diskrit dengan 2
kejadian yang berkomplemen, seperti distribusi binomial.
Ciri
dari Hipergeometrik :
Terdapat populasi sebanyak N
dan terdapat sebanyak r kategori A. Dari populasi ini, diambil sebuah sampel
acak berukuran n. Dari sampel berukuran n tsb akan diketahui peluang bahwa
terdapat sebanyak x buah kategori A.
Rumus Distribusi
Hipergeometrik

p(x)/h(x)
= probabilitas x sukses dalam n percobaan
n
= jumlah percobaan
N
= jumlah elemen dalam populasi
r
= jumlah elemen dalam populasi yang
sukses
b) Distribusi Multinomial
Bila
suatu percobaan binomial menghasilkan lebih dari dua kemungkinan seperti
suka, tidak suka, cukup suka maka percobaan itu menjadi percobaan Multinomial.
Rumus Distribusi Multinomial



Contoh
Distribusi Multinomial
Dadu
seperti pada contoh 3 digelindingkan 3 kali.
a.Berapakah
peluang mendapatkan 0 atau 1 sisi C 2 kali dan peluang mendapatkan 2 atau 3
sisi C 1 kali
b.Berapakah
peluang mendapatkan 0 atau 1 sisi C 1 kali dan peluang mendapatkan 2 atau 3
sisi C 2 kali
Penyelesaian
a.
b.
Distribusi Peluang Untuk Variabel
Kontinu
1) Distribusi Normal
Distribusi normal adalah distribusi dari
variabel acak kontinu. Kadang-kadang distribusi normal disebut juga
dengan distribusi Gauss. Distribusi ini merupakan distribusi yang paling
penting dan paling banyak digunakan di bidang statistika.
Fungsi densitas distribusi normal diperoleh dengan
persamaan sebagai berikut

dimana
π =
3,1416
e =
2,7183
µ =
rata-rata
σ =
simpangan baku
Persamaan
di atas bila dihitung dan diplot pada grafik akan terlihat seperti pada Gambar
berikut.

Sifat-sifat
penting distribusi normal adalah sebagai berikut:
1.
Grafiknya selalu berada di atas sumbu x
2.
Bentuknya simetris pada x = µ
3.
Mempunyai satu buah modus, yaitu pada x = µ
4.
Luas grafiknya sama dengan satu unit persegi, dengan rincian
a.
Kira-kira 68% luasnya berada di antara daerah µ – σ dan µ + σ
b.
Kira-kira 95% luasnya berada di antara daerah µ – 2σ dan µ + 2σ
c.
Kira-kira 99% luasnya berada di antara daerah µ – 3σ dan µ + 3σ
Membuat
kurva normal umum bukanlah suatu pekerjaan yang mudah. Lihat saja rumus
untuk mencari fungsi densitasnya (nilai pada sumbu Y) begitu rumit. Oleh
karena itu, orang tidak banyak menggunakannya. Orang lebih banyak menggunakan DISTIBUSI
NORMAL BAKU.
Kurva
distribusi normal baku diperoleh dari distribusi normal umum dengan cara
transformasi nilai x menjadi nilai z, dengan formula sbb:

Kurva
distribusi normal baku disajikan pada Gambar berikut ini.

Gambar 2.
Kurva distribusi normal baku
|
Kurva
distribusi normal baku lebih sederhana dibanding kurva normal umum. Pada
kurva distribusi normal baku, nilai µ = 0 dan nilai σ=1, sehingga terlihat
lebih menyenangkan. Namun, sifat-sifatnya persis sama dengan sifat-sifat
distribusi normal umum.
Untuk
keperluan praktis, para ahli statistika telah menyusun Tabel distribusi normal
baku dan tabel tersebut dapat ditemukan hampir di semua buku teks
Statistika. Tabel distribusi normal bakui disebut juga dengan Tabel Z dan
dapat digunakan untuk mencari peluang di bawah kurva normal secara umum, asal
saja nilai µ dan σ diketahui. Sebagai catatan nilai µ dan σ dapat diganti
masing-masing dengan nilai  dan
S.
dan
S.
2)
Distribusi Student
Adalah pengujian hipotesis yang menggunakan
distribusi T sebagai uji statsistik, table
pengujiannya
disebut table T student.
Ciri-cirinya
adalah :
·
jumlah sample biasanya kurang dari 30 (n <
30)
· Distribusi t-student seperti distribusi Z
berbentuk genta atau lonceng dan simetris dengan nilai rata rata sama dengan 0
· Distribusi t-student bukan merupakan satu
kurva seperti kurva Z, tetapi keluarga dari distribusi t. setiap
distribusi t mempunyai rata-rata hitung sama dengan 0,tetapi dengan standar deviasi
yang berbeda-beda,sesuai dengan besarnya
sampel (n).
Rumus:

dimana
:
t :
Nilai Distribusi t
µ :
Nilai rata-rata populasi
x
bar :
Nilai rata-rata sampel
s :
Standar deviasi sampel
n :
Jumlah sampel
3)
Distribusi Chi Square
Chi square adalah pengujian
hipotesis mengenai perbandingan antara frekuensi observasi atau yang
benar-benar terjadi atau aktual dengan frekuensi harapan. Yang dimaksud dengan
frekuensi harapan adalah frekuensi yang nilainya dapat di hitung secara
teoritis (e). sedangkan dengan frekuensi observasi adalah frekuensi yang
nilainya di dapat dari hasil percobaan (o).
Karakteristik Chi‐Square:
§ Nilai
Chi‐Square selalu positip.
§ Terdapat
beberapa keluarga distribusi Chi‐Square, yaitu
distribusi Chi‐Square dengan
DK=1, 2, 3, dst.
§ Bentuk
Distribusi Chi‐Square adalah menjulur positip.Semakin
besar derajat bebas, semakin mendekati distribusi normal.
§ df
= k – 1, dimana k adalah jumlah katagori. Jadi bentuk distribusi chi square
tidak ditentukan banyaknya sampel, melainkan banyaknya derajat bebas.
Rumus:
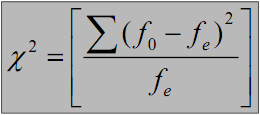
Dimana
:
χ2 : Nilai chi-kuadrat
fe : Frekuensi yang
diharapkan
fo : Frekuensi yang diperoleh/diamati
Distribusi F merupakan
distribusi probabilitas kontinyu. [1][2][3][4]Distribusi
F juga dikenal dengan sebutan distribusi F Snedecor atau distribusi
Fisher-Snedecor (setelah R.A.
Fisher dan George W. Snedecor).
Distribusi F seringkali digunakan dalam pengujian statistika, antara lainanalisis
varians dan analisis
regresi,distribusi ini juga mempunyai variabel acak yang
kontinu.
Ciri-Ciri Distribusi F adalah:
·
Distribusi F tidak pernah mempunyai nilai
negatif sebagaimana pada distribusi Z. Distribusi
Z mempunyai nilai positif di
sisi kanan dan negatif sisi kiri nilai tengahnya.
·
Nilai distribusi F mempunyai rentang dari tidak terhingga sampai 0. Apabila nilai F meningkat, maka distribusi F mendekati sumbu X, namun tidak pernah menyentuh sumbu X tersebut.
Rumus:

Dimana
:
F =
Variabel acak yang memenuhi F>0
K =
bilanan tetap yang harganya pada derajat kebebasan v1 dan v2
V1 =
Derajat kebebasan antara varians rata-rata sampel (sebagai pembilang)
V2 =
derajat kebebasan dalam keseluruhan sampel (sebagai penyebut)
Luas
dibawah kurva satu.
Daftar
distribusi normal berisikan nilai-nilai F untuk peluang 0,01 dan 0,05 dengan
derajat
kekebasan v1 dan v2. Peluang ini sama dengan luas daerah ujung kanan yang
diarsir,
sedangkan derajat kekebasan pembilang (v1 ) ada pada baris paling atas dan
derajat
kebebasan penyebut (v2) pada kolom paling kiri.

Notasi
lengkap untuk nilai-nilai F dari daftar distribusi F dengan peluang p dan
dk = (v1,v2) adalah Fp(v1,v2). Demikianlah untuk
contoh kita didapat :
F0.05(24,8) = 3.12
dan F0,01(24,8 )= 5.28.
Meskipun
daftar yang diberikan hanya untuk peluang p = 0.05 dan p = 0.01, tetapi
sebenarnya masih bisa didapat nilai-nilai F dengan peluang 0,99 dan 0,95. Untuk
ini digunakan hubungan :

Dalam rumus diatas perhatikan antara p dan
(1- p) dan pertukaran antara derajat kebebasan (v1, v2 )
menjadi (v2, v1).